| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 고전방법론
- 자연어처리
- 통계적품질관리
- 경제용어
- 인공지능
- 공대생의전공공부
- 일일경제공부
- 메타휴리스틱
- 공대생의연구공부
- 특허
- 공대생의경제공부
- 정보시스템
- 정보시스템설계및분석
- 언어학
- 공대생의문과공부
- 확률기반자연어처리
- 국어국문학
- 산업공학
- 공대생의언어학공부
- 언어적지식
- 영어영문학
- 통계학
- 최적화기법
- 최적화문제
- 이공계를위한특허이해
- 지적재산권
- 컴퓨터공학
- 지식재산경영
- 공대생의산업공학공부
- 품질경영
- Today
- Total
Fintecuriosity
[메타 휴리스틱] 단일해 기반 메타휴리스틱스 본문
이번 글의 내용은 전남대학교 산업공학과 김여근 교수님의 메타휴리스틱 교재 정리 및 참조하였음을 먼저 밝힙니다.
(다른 참조한 논문과 자료들은 아래에 기재되어 있습니다.)
이 포스트는 "메타 휴리스틱" 책의 내용을 참조 및 공부한 것을 바탕으로 제가 이해한 정보를 추가하여 쓰여졌습니다.
혹시 제가 잘못 알고 있는 점이나 보완할 점 있다면 댓글로 알려주시면 감사하겠습니다.
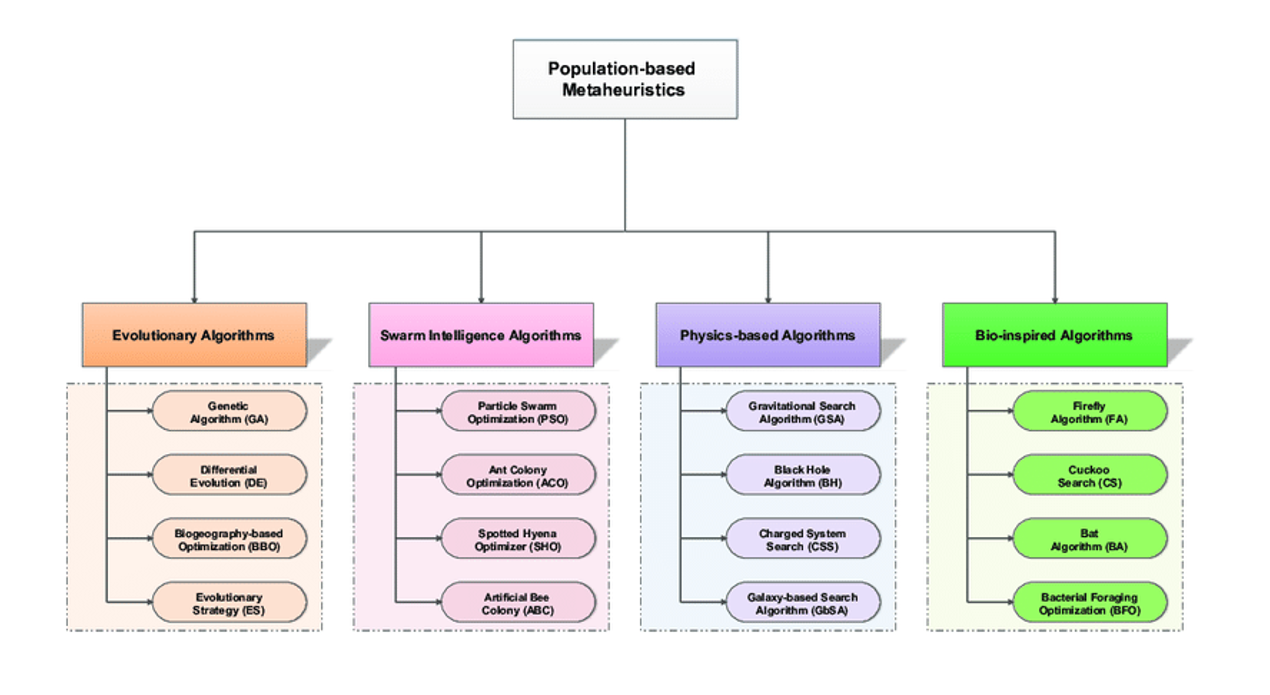
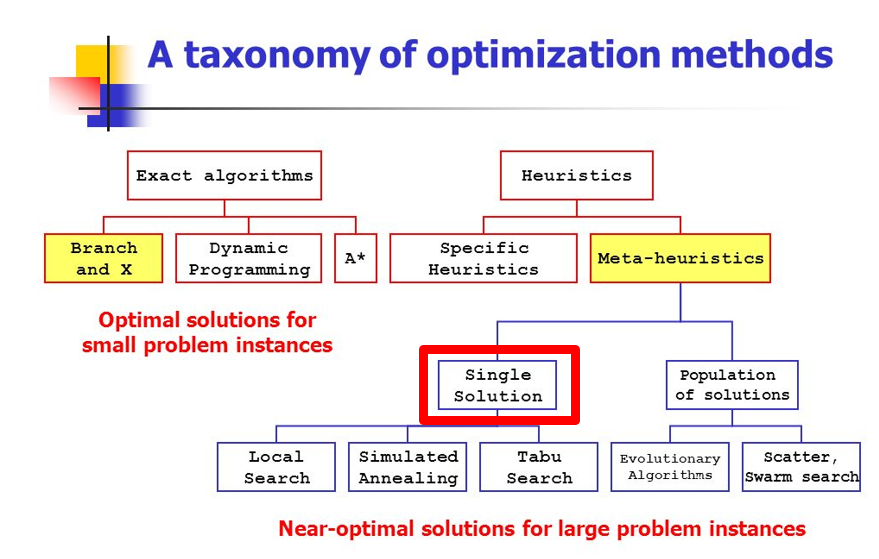
단일해 기반 메타휴리스틱스(S-MHs)에서는 단일 현재해의 이웃에서 어떤 기준에 의해 하나의 해(이웃해)를 선택하고, 그 해로 이동하면서 해 공간을 탐색해 나갑니다.
그러므로 S-MHs를 설계할 때는 이웃을 반드시 정의해야 합니다. 즉 이웃 구조를 결정해야 하는 것입니다. 이웃 구조는 성능에 크게 영향을 줍니다. S-MHs가 성공적으로 문제를 해결하기 위해서는 다루는 문제에 이웃 구조가 적절해야 합니다. 이웃 구조는 사용하는 S-MHs보다는 다루는 문제에 종속됩니다.

해 x의 이웃을 N(x)로 나타내고, 해 x의 이웃에 속한 해 x', 즉 x' ∈ N(x)를 해 x의 이웃해(neighbor)라 부릅니다. 이웃해 x'는 해 x를 조금 변경하는, 즉 근접 변환(perturbation)하는 '이동(move) 연산을 적용하여 생성됩니다. 이웃의 성질을 '지역성(locality)'으로 나타낼 수 있습니다. 해의 표현이 조금 변경될 때, 해도 조금 변화되어야 합니다. 이러한 경우 이웃은 '강한 지역성'을 가지고 있다고 하고, S-MHs도 이러한 문제에서 의미 있는 탐색을 하게 됩니다. 이와 달리 조그만 표현의 변화에도 해가 큰 영향을 받으면, 이는 '약한 지역성'이라 하고, 이 경우 S-MHs는 잘 작동하지 않습니다. 지역성이 아주 약하면 임의 탐색과 유사하게 됩니다.
이웃의 정의는 주로 해의 표현(encoding)에 종속됩니다. 연속 최적화 문제에서 실수로 해를 표현하면 해 x의 이웃 N(x)는 중심이 x이고 반경이 ε(>0)인 구(球)로 정의할 수 있습니다. 이렇게 정의하면 해 x에서 거리가 ε이내인 모든 점이 해 x의 이웃이 됩니다. 또한 이산 최적화 문제에서 이진수(binary)로 해를 표현하면 이웃을 해밍(hamming)거리로 정의할 수 있습니다. 이진수 표현에서 해밍(hamming)거리 1을 이웃으로 정의하면, (0000)의 이웃은 (1000), (0100), (0010), (0001)입니다.
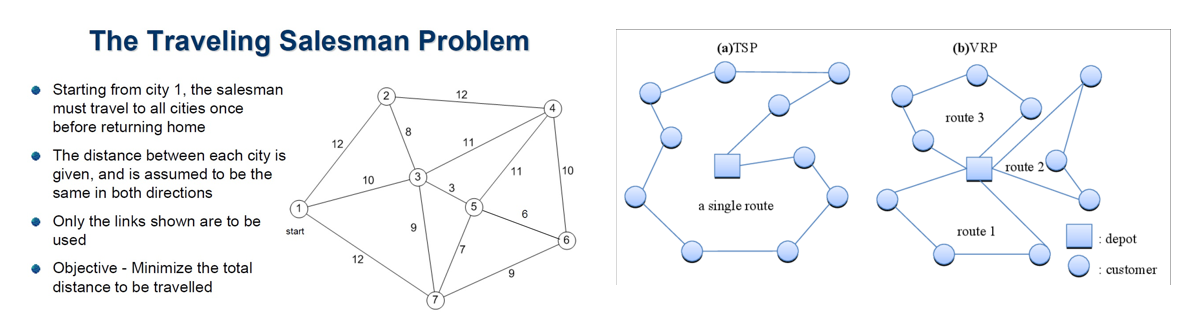
표현은 다루는 문제의 특성을 잘 나타낼 수 있어야 합니다. 문제의 특성을 잘 반영한 표현은 해를 변환할 때, 즉 해를 이동할 때 좋은 해를 유도할 수 있는 이웃 구조를 사용할 수 있기 때문입니다. 외판원 문제(traveling salesman problem: TSP), 흐름생산계획 등 순서 문제에서는 순열표현이 흔히 사용됩니다. 예로 항상 본사 0에서 출발하여 7개의 도시를 거쳐 본사 0으로 돌아오는 외판원 문제를 살펴보겠습니다. 본사 0에서 도시 3-5-7-1-6-4-2의 순서로 방문하여 본사 0으로 돌아온다면 이를 (3,5,7,1,6,4,2)와 같은 순열로 표현할 수 있습니다.

이와 같은 순열표현에서는 두 인자 위치를 교환하는 교환(swap) 변환, 한 인자를 다른 위치로 이동하는 삽입(insertion) 변환, 인접하는 두 인자의 위치를 바꾸는 인접 교환(adjacent swap) 변환, 특정 부분경로의 순서를 거꾸로 하는 역순(inversion) 변환, k-opt 변환은 Hamiltonian 순환로 상에서 k 개의 호를 제거하고 (k=2, 3 , ... , n), 순환로 상에 없는 k개의 호를 대체하여 새로운 Hamiltonian 순환로를 만드는 변환입니다. 또한 그래프로 표현된 경우, 호의 추가와 삭제(k개 호 추가와 k개 호 삭제, k=1,2,...) , 마디의 삭제와 추가, 이 외에 여러 형태의 호와 마디 변경을 이웃으로 정의할 수 있습니다.
문제의 크기가 커지면 이웃의 크기가 커집니다. 이웃의 크기가 커지면 이웃 탐색에 계산량이 많아지게 됩니다. 탐색 횟수나 계산소요시간이 한정된 경우에 이웃해를 모두 탐색하는 것은 지역 탐색에 치중하는 결과를 가져올 수 있습니다. 즉, 다른 영역의 탐사와 불균형을 이룰 수 있습니다.
긴글 읽어주셔서 감사합니다.
[References]
[1] Y. Kim. (2017). 메타휴리스틱스, Metaheuristics
[2] Nanda, S. J., & Panda, G. (2014). A survey on nature inspired metaheuristic algorithms for partitional clustering. Swarm and Evolutionary Computation, 16, 1–18.
[3] Bolduc, M., Renaud, J., Boctor, F. et al. A perturbation metaheuristic for the vehicle routing problem with private fleet and common carriers. J Oper Res Soc 59, 776–787 (2008).
'Industrial Engineering > 메타휴리스틱' 카테고리의 다른 글
| [메타 휴리스틱] 비가능해 버리기 전략(reject strategy) (0) | 2020.09.30 |
|---|---|
| [메타 휴리스틱] 집단 기반 메타휴리스틱스 (0) | 2020.09.30 |
| [메타 휴리스틱] 메타휴리스틱 알고리즘 종료조건 (0) | 2020.09.28 |
| [메타 휴리스틱] 메타휴리스틱스에서의 파라미터 조정 (0) | 2020.09.28 |
| [메타 휴리스틱] 메타휴리스틱스에서의 초기해 (0) | 2020.09.28 |




