| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 메타휴리스틱
- 언어학
- 지식재산경영
- 언어적지식
- 특허
- 공대생의경제공부
- 최적화문제
- 통계적품질관리
- 이공계를위한특허이해
- 자연어처리
- 국어국문학
- 지적재산권
- 산업공학
- 컴퓨터공학
- 일일경제공부
- 영어영문학
- 공대생의산업공학공부
- 공대생의연구공부
- 통계학
- 공대생의문과공부
- 인공지능
- 최적화기법
- 공대생의전공공부
- 고전방법론
- 공대생의언어학공부
- 확률기반자연어처리
- 정보시스템설계및분석
- 경제용어
- 품질경영
- 정보시스템
- Today
- Total
Fintecuriosity
[패턴인식] 선형대수와 확률통계 review_part 5 본문

이번 글의 내용은 고려대학교 컴퓨터공학과 김승룡 교수님과 산업경영공학과 정태수 교수님의 강의 정리 및 참조하였음을 먼저 밝힙니다. (다른 참조한 논문과 자료들은 아래에 기재되어 있습니다.)
혹시 제가 잘못 알고 있는 점이나 보완할 점 있다면 댓글로 알려주시면 감사하겠습니다.
◎ Probability in Machine Learning
- Probability is the study of uncertainty
- Probability(확률론)은 불확실성에 대해 공부하는 분야입니다.
- Probability is at the heart of machine learning algorithms
- 머신러닝 알고리즘에서 핵심은 확률론입니다.
- Most machine learning methods involves the use of random variable and probability distributions
- 대부분의 머신러닝 방법론들은 확률분포와 확률변수들이 포함되어 있습니다.
- Many unsupervised methods use discrete probability distributions and Bayesian analysis
- 많은 비지도 학습 방법론에서 이산 확률 분포와 베이지안 분석 기법이 기반이 되고 사용됩니다.

◎ Random Variable
- Random variables are variables which takes on values according to a probability distribution(randomly)
- 확률변수는 확률분포에 기반하여 값들을 나타내는 변수입니다.(무작위로)
- define X = {x1, x2, x3, .... , xn}이 위의 개념에 대한 예제입니다.
- 각 x_i ~ N(μ,σ)는 무작위로 분포에서 뽑은 것으로 생각할 수 있습니다.
- (in this case the Gaussian) 정규, 가우시안 분포에서 μ,σ 매개변수, 즉 평균과 편차를 가지고 있는 것입니다.

◎ Random Variables
- Random variables can be discrete, taking on a finite or countably infinite numbers of value
- 확률 변수가 이산적인 상태를 가질때는 유한 or 셀수있는 무한의 값으로 표현할 수 있습니다.
- Continuous taking on an infinite number of values
- 확률 변수가 연속적인 상태를 가질때는 무한의 값으로 표현할 수 있습니다.
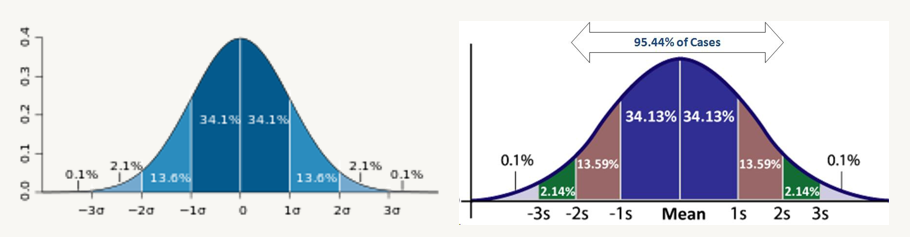
◎ Probability Distributions
- 확률분포는 likelihood(공산)을 설명해주는데, likehood를 통해 확률 변수는 정해진 값을 가집니다.
- Discrete random variables are described by probability mass functions(PMFs)
- Continuous random variables are described by probability density functions(PDFs)
◎ Properties of PMFs and PDFs
* A PMF is a function P that must satisfy

*A PDF is a function p that must satisfy

◎ Marginal Probability

- 2가지의 확률변수(x, y)가 주어졌을때 우리는 오직 한개 변수의 분포도에 대해서만 관심을 가질 수 있음.
☞ 더욱 쉬운 예제를 들어보자면
- 결합 확률 분포 함수가 주어진 상태에서 오직 한가지 확률 변수의 확률 분포만을 알고 싶은 경우가 있다.
- 가령 두 개의 확률 변수 X,Y에 대하여 결합 확률 함수 혹은 결합 확률 밀도 함수가 다음과 같이 주어져있다고 가정
※ 이러한 확률 밀도 함수로부터 알고 싶은 정보가 만약 X 하나라면, Y에 대한 정보는 필요없게 된다.
- 이 때 수행하는 것이 marginalization이다.
※ 방법은 다음과 같다.
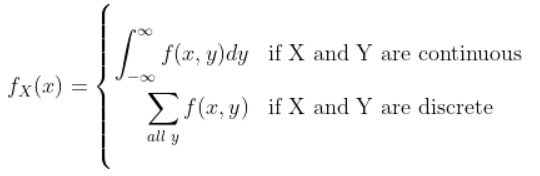
따라서 결합 확률 밀도 함수로부터 한가지 확률 변수에 대한 정보만 알고 싶다면
marginal pmf 또는 marginal pdf를 사용하면 된다.

◎ Conditional Probability
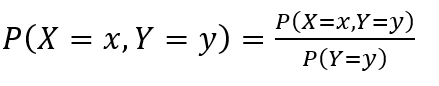
- 우리는 자주 어떠한 일이 생길 가능성에 관심을 가집니다.
- 이를 조건부 확률에 빗대어 설명을 할 수 있습니다.
- 조건부 확률은 2개의 사건에 대한 확률을 설명할 수 있습니다.
- 하나의 확률 변수가 주어졌을 때 다른 확률 변수에 대한 확률입니다.
ex) 어떠한 사건 Y가 발생했을 때 사건 X가 일어날 확률을 의미합니다.
긴 글 읽어주셔서 감사합니다.
References
[1] S. Kim (2020). Graduate Course
[2] T.Jung (2020). Graduate Course
'Artificial Intelligence > 패턴인식' 카테고리의 다른 글
| [패턴인식] 선형대수와 확률통계 review_part 4 (0) | 2020.07.31 |
|---|---|
| [패턴인식] 선형대수와 확률통계 review_part 3 (0) | 2020.07.26 |
| [패턴인식] 선형대수와 확률통계 review_part 2 (0) | 2020.07.24 |
| [패턴인식] 선형대수와 확률통계 review_part 1 (0) | 2020.07.23 |
| [패턴인식] Introduction (0) | 2020.07.22 |




